Memoization (Advanced)
We won't go into great detail here, but we will look at improving the efficiency of the Fibonacci numbers. This is a reasonably advanced topic.
There are two ways of doing this.
One is simply the bottom-up approach. Instead of writing recursively, we just write this with a loop.
The other is by making recursion more efficient.
Sometimes a recursive algorithm is just easier to write, so looking for improvements on speed and memory are important.
To demonstrate this, try the following:
import timeit
def fib(n):
if n < 2:
return 1
return fib(n-1) + fib(n-2)
start_time = timeit.default_timer()
# call the function
fib(35)
end_time = timeit.default_timer()
print(end_time - start_time) # You will get about 5 seconds for this. That is slow!!!
You will get about 5 seconds for this. That is slow!!!
import timeit
def fib_loop(n):
if n < 2:
return 1
fib0 = 1
fib1 = 1
while n > 2:
temp = fib1
fib1 = fib1 + fib0
fib0 = temp
n -= 1
return fib1
start_time = timeit.default_timer()
# call the function
fib_loop(35)
end_time = timeit.default_timer()
print(end_time - start_time) # You will get a fraction of a second for this. That is much faster!!!
You will get a fraction of a second for this. That is much faster!!!
In fact as soon as you go beyond about 36 it starts to take a long long time.
This is the essence of something called computational efficiency. Sometimes our algorithms are just plain bad and slow!
It doesn't matter if we have the worlds fastest machine, in some cases, it just won't complete.
What is Going On?
The recursive approach continues to call the function until it hits a base case. In the cases of the fibonacci, this is actually a tree of function calls.
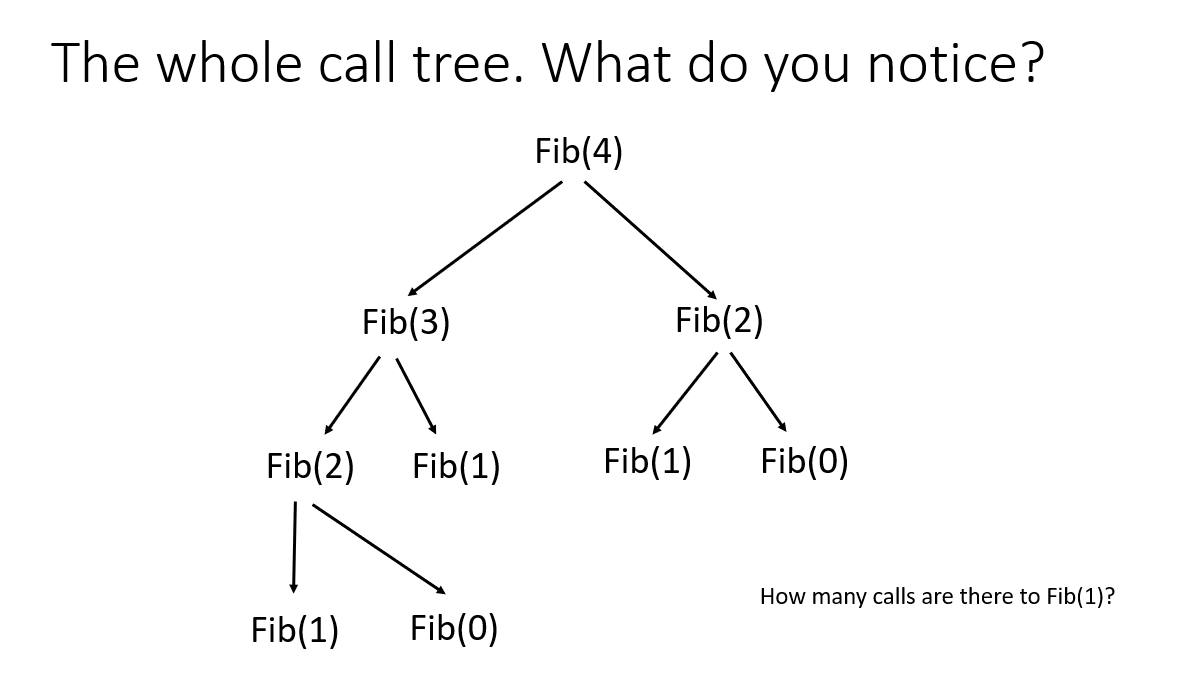
What you should notice is that there are multiple calls to the fib() function for fib(2), fib(1) and fib(0). This takes time.
The key to making this faster is that when we make a call to a function with a given value, e.g. fib(1), we store the result in a dictionary and then when we try to call it again, instead of using recursion, we just look up the result in the dictionary.
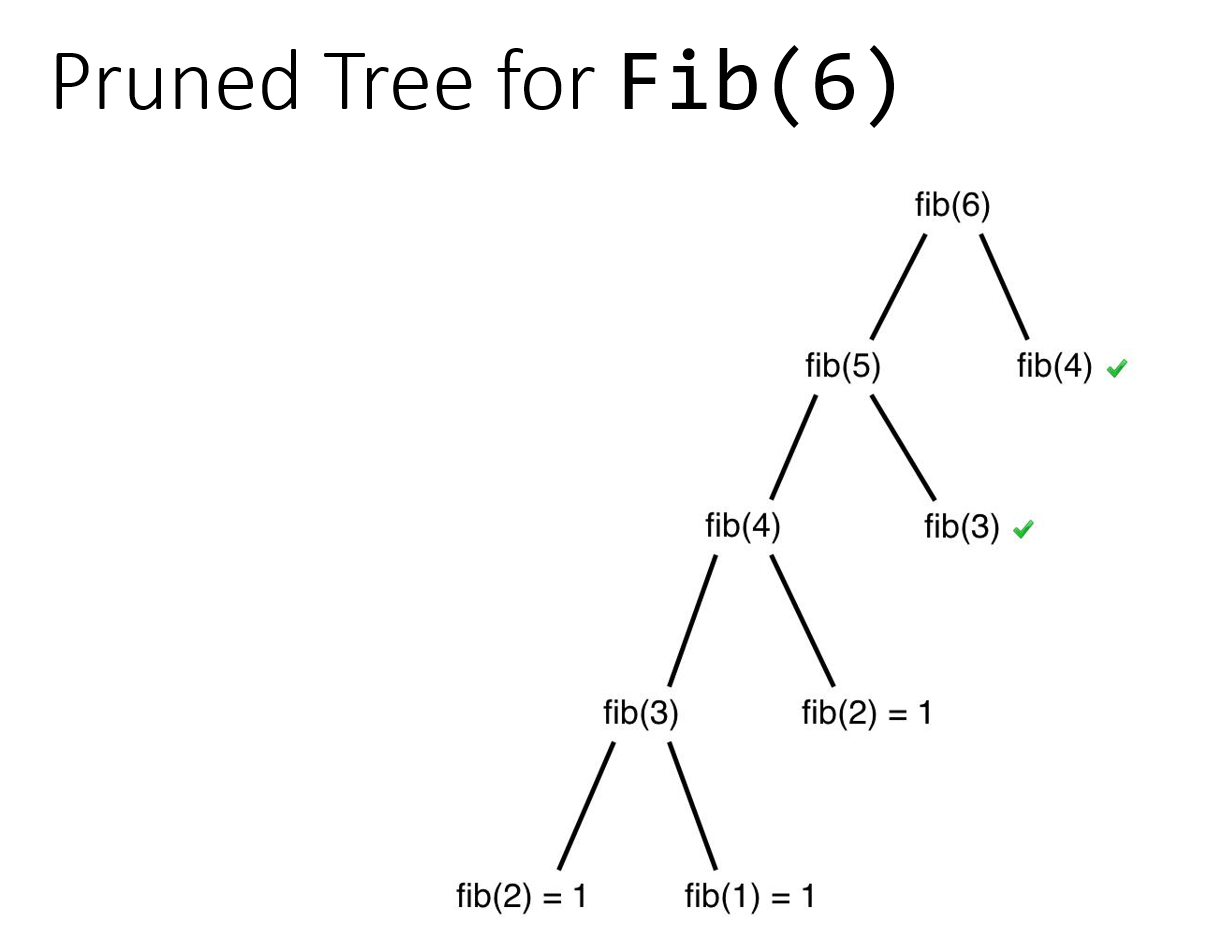
I would read the following article for a more in depth explanation.
Memoization
To code this in Python we can save a fib number everytime we see it and then if we see it again we just look it up, we don't do the expensive function call!
Here is the code. The function fib_memo uses a dictionary memo to keep track of the fib numbers. I strongly recommend that you paste this into Python Tutor.
import timeit
def fib_memo(n, memo):
# if not seen add to dictionary
if not n in memo.keys():
# add unseen to dictionary
if n < 2:
memo[n] = 1
else:
memo[n] = fib_memo(n-1, memo) + fib_memo(n-2, memo)
return memo[n]
fib_nums = {}
start_time = timeit.default_timer()
# call the function
fib_memo(35, fib_nums)
end_time = timeit.default_timer()
print(end_time - start_time) # You will get a fraction of a second for this. That is much faster!!!
Analysing all 3 Approaches
The program below will output the following plot using Python's plotting library matplotlib.
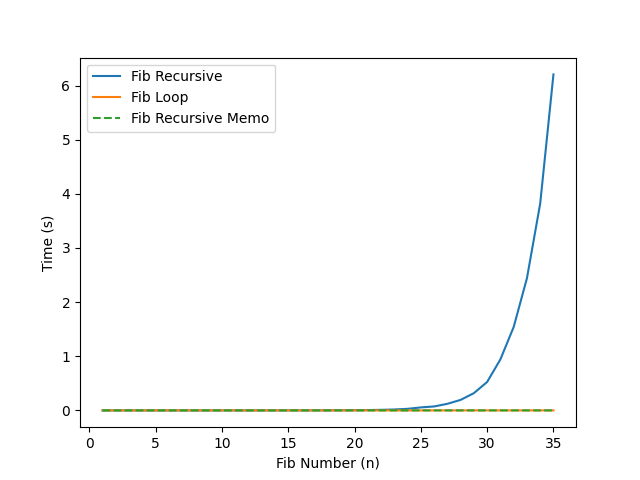
You can clearly see here that the the recursive approach is very poor after only 36.
Thus, you can use the other approaches to generate much much larger Fibonacci numbers.
import timeit
import matplotlib.pyplot as plt
def fib(n):
if n < 2:
return 1
return fib(n-1) + fib(n-2)
def fib_loop(n):
if n < 2:
return 1
fib0 = 1
fib1 = 1
while n > 2:
temp = fib1
fib1 = fib1 + fib0
fib0 = temp
n -= 1
return fib1
def fib_memo(n, memo):
# if not seen add to dictionary
if not n in memo.keys():
# add unseen to dictionary
if n < 2:
memo[n] = 1
else:
memo[n] = fib_memo(n-1, memo) + fib_memo(n-2, memo)
return memo[n]
def time_function(func, n, memo=None):
start_time = timeit.default_timer()
if not memo == None:
func(n, memo)
else:
func(n)
end_time = timeit.default_timer()
return end_time - start_time
fib_nums = {}
cases = range(1,36)
times_fib = []
times_fib_loop = []
times_fib_memo = []
for n in cases:
print(f"Computing times for n={n}")
times_fib.append(time_function(fib, n))
times_fib_loop.append(time_function(fib_loop, n))
times_fib_memo.append(time_function(fib_memo, n, memo=fib_nums))
plt.plot(cases, times_fib)
plt.plot(cases, times_fib_loop)
plt.plot(cases, times_fib_memo, '--')
plt.xlabel("Fib Number (n)")
plt.ylabel("Time (s)")
plt.legend(["Fib Recursive", "Fib Loop", "Fib Recursive Memo"])
plt.show()
=== TASK ===
Please note that this is an advanced topic and you are by no means expected to be able to do this straight away. In fact you shouldn't worry if you can't complete it. If you are struggling then I would move on.
We have a grid. Your goal is to walk through the grid from start to finish by only moving right or down.
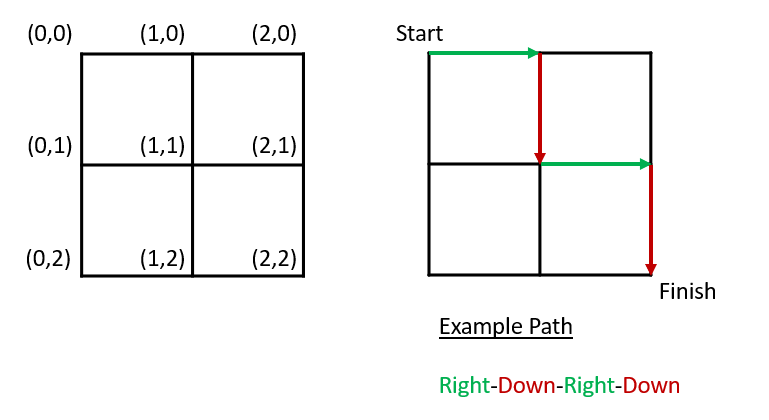
How many paths are there from the start to the finish given that we can move right or down?
For the two by two grid given in the example we have the following paths.
RRDD
RDRD
RDDR
DRRD
DRDR
DDRR
To solve this we can turn to recursion.
If we look at the number of paths at the end (2,2) we can note that they will actually be the sum of the number of paths to (1,2) and (2,1).
Similarly the number of paths from (1,2) are the sum of the number of paths to (0,2) and (1,1).
The number of paths on the edge, such as (0,2) are the just the number of paths from (0,1) (that is you can only get to (0,2) from (0,1).
Once we get back to the start (0,0) there is just 1 path, that is, the start.
We actually have the following:
if we are not on an edge
no_paths(x,y) = no_paths(x-1,y) + no_paths(x,y-1)
if we are on an edge left x = 0
no_paths(0,y) = no_paths(0, y-1)
if we are on an edge left y = 0
no_paths(x,0) = no_paths(x-1, 0)
if we are at the start (0,0)
no_paths(0,0) = 1
We can now write this as a recursive function as follows:
def no_paths(x,y):
if x == 0 and y == 0:
return 1
elif x == 0:
return no_paths(0, y-1)
elif y == 0:
return no_paths(x-1, 0)
else:
return no_paths(x-1, y) + no_paths(x, y-1)
print(no_paths(1,1)) # prints 2
print(no_paths(2,2)) # prints 6
print(no_paths(1,2)) # prints 3
Copy and paste the following into a new Python file to get started.
You need to fix the paths_memo() function so that it uses memoization. This will mean that it will run extremely quickly, where as trying to run larger numbers for paths will take a long time or never end.
import timeit
def no_paths(x,y):
if x == 0 and y == 0:
return 1
elif x == 0:
return no_paths(0, y-1)
elif y == 0:
return no_paths(x-1, 0)
else:
return no_paths(x-1, y) + no_paths(x, y-1)
def no_paths_memo(x, y, memo):
pass
if __name__ == "__main__":
# This times the paths method
start_time = timeit.default_timer()
# walk a grid 13 by 13. This takes approximately 2.5 seconds
print(f"Number of paths for a 13x13 grid is {no_paths(12,12)}")
end_time = timeit.default_timer()
print(f"Time taken: {end_time - start_time}")
# This times the paths_memo method
start_time = timeit.default_timer()
# walk a grid 13 by 13. This should take a fraction of a second
print(f"Number of paths for a 13x13 grid is {no_paths_memo(12,12, {})}")
end_time = timeit.default_timer()
print(f"Time taken: {end_time - start_time}")